Rotating Reference Frames
Let the X-Y coordinate system be inertial and fixed and the x-y coordinate system be a body-fixed coordinate system that may translate and rotate as shown in the figure.
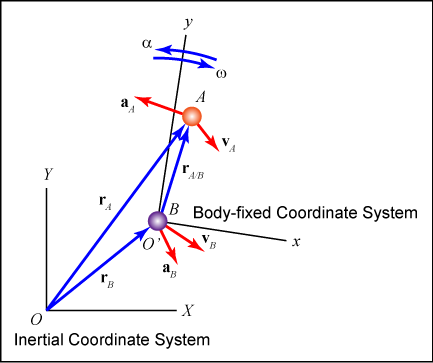
If the x-y coordinate system translates and rotates, the derivatives of the unit-direction vectors may not equal zero. This fact provides different equations for a particle's velocity and acceleration in terms of the rotating reference frame.
- Position: rA = rB + rA/B = rB + (xi + yj)
- Velocity: vA = vB + vA/B = vB + vA,rel + ω x rA/B
- Acceleration: aB = aB + aA/B = aB + aA,rel + α x rA/B - ωCD2 rB/C + 2ω x vA,rel
